Math

Through mathematics at JCHS, students explore the connections that mathematics have to other academic disciplines and to problems from the real world.

Our approach to math instruction is informed by research by Dr. Jo Boaler and Dr. Peter Liljedahl, which has shown consistently that students learn the most when they are grappling with hard problems and feel some “productive discomfort.” While all math classes at JCHS include some traditional, direct instruction, our teachers emphasize students playing an active role in their own learning and engaging with unfamiliar, difficult problems.

Our math classes require students to lean into this productive discomfort, where students learn to think like mathematicians and explore unfamiliar concepts through discovery-based problem-solving. This requires students to embrace mistakes as essential to the learning process and work with peers along their journey.

Understanding the Differences in Course Levels

At-Level Math Classes

These classes focus on building foundational skills in the core high school mathematical disciplines of Elementary Algebra, Geometry, Advanced Algebra, Precalculus, and/or Statistics. These classes emphasize procedural fluency and repeated practice of those skills that will most critically serve students in college and beyond. These classes also move at a more measured pace and ensure students are prepared for the next level class.

These classes emphasize the development of a “mathematical mindset” by introducing students to unfamiliar problems on a regular basis. Students work with peers on discovery-based problem-solving activities with direct teacher support.

Advanced and AP Math Classes

These classes aim to help students build advanced problem-solving skills that they will need during and after AP Calculus, in particular those students who aspire to highly selective STEM programs. While these classes do cover more material and move at a more rapid pace than the corresponding at-level class, the key difference is more one of attitude and approach.

These classes emphasize the development of a “mathematical mindset” by challenging students to tackle difficult and unfamiliar problems on a daily basis. In small groups, students learn to explore new topics with minimal direction from the teacher. Initially, this often feels challenging because it requires students to think deeply and be open to trying different approaches than those that they may have used in previous classes.

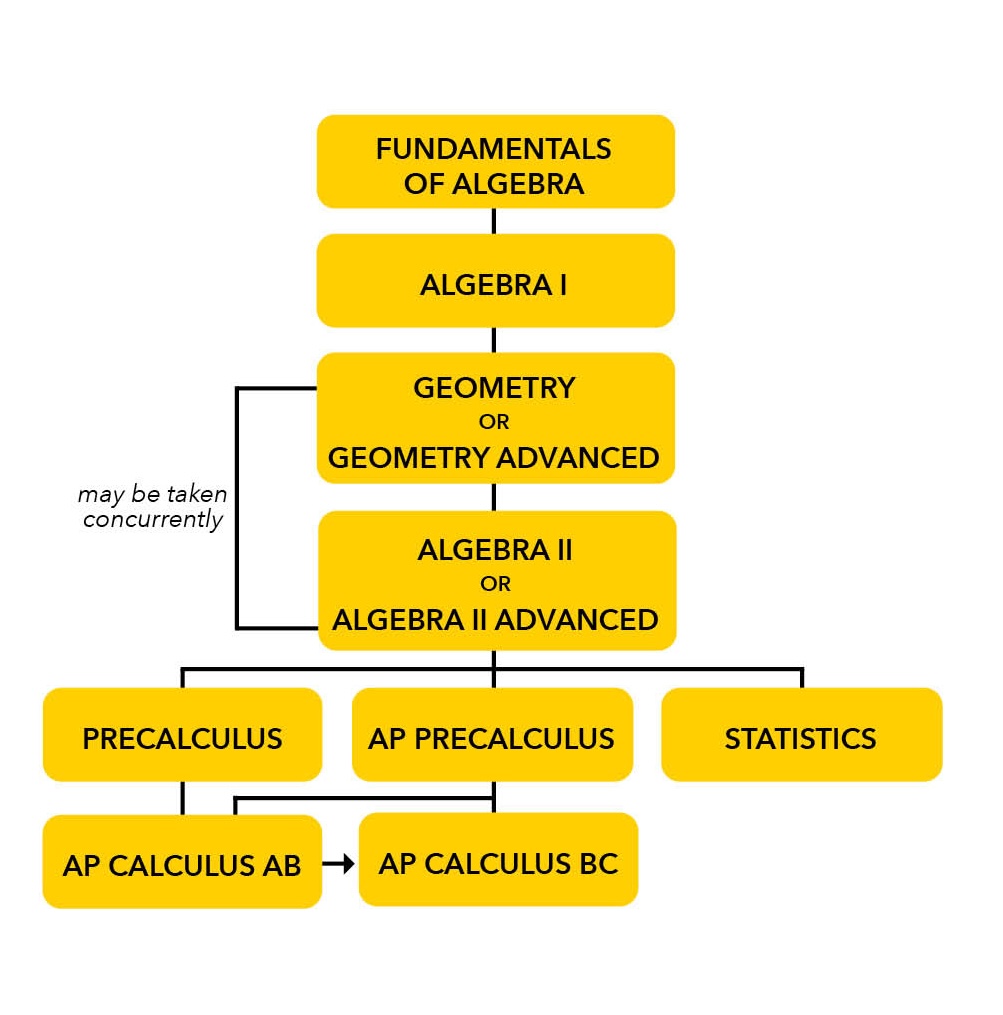
Math Requirements: All students must complete three years of core math courses through at least Algebra II. A course matching assessment is used to determine the appropriate level of math for each incoming student. Mastery of algebra is foundational for success in high school math and science, and many ninth graders at JCHS enroll in Algebra I. Students who excel in Algebra I and wish to reach AP Calculus in high school may, with department approval, either complete a summer Geometry course followed by Algebra II Advanced, or enroll in Geometry and Algebra II Advanced concurrently as 10th graders.

CORE COURSES

This small, highly personalized class is designed for students who need extra support mastering pre-algebra and middle school math concepts to provide a solid foundation for future success in Algebra I and other high school math classes. Students will work with hands-on mathematical tools such as algebra tiles to help conceptualize skills involving solving equations and all topics surrounding quadratic functions.

This problem-based Algebra I course invites students to deepen their mathematical understanding through real-world applications. In this student-centered environment, learners work collaboratively and at their own pace to develop critical thinking skills. Our discourse-rich curriculum provides accessible entry points for students of all abilities, offering highly differentiated lessons with enrichment opportunities built into every unit. Core topics include linear and exponential functions, systems of equations, and an introduction to quadratic equations.

Prerequisite(s): Algebra I

This course is an introduction to Euclidean geometry. There is an emphasis on developing a student’s understanding of mathematical theory, problem solving, and the ability to write clear, logical arguments based on definitions, postulates, and theorems. Geometry is explored through many modalities, including algebra, formal and informal proof, compass construction, architecture, and origami.

Prerequisite(s): Algebra I and Department Approval

This course offers an in-depth study of the properties and applications of common geometric figures in both two and three dimensions, where students will engage in the study of transformations and right triangle trigonometry, employing both inductive and deductive thinking skills in problem-solving situations. Additionally, the course places a strong emphasis on writing proofs to solve and prove properties of geometric figures, fostering a deep understanding of Euclidean Geometry. Complementing this traditional focus, we also introduce elements of non-Euclidean geometries, dedicating a portion of our curriculum to exploring innovative concepts like Finite Affine Geometry and Projective Geometry through interactive games like SET and Spot It!. This blend of traditional and modern geometrical studies not only solidifies a strong foundation in mathematical concepts but also encourages creative thinking and a deeper appreciation for the subject’s complexity and beauty, preparing students for advanced mathematical pathways.

Prerequisite(s): Geometry

This course focuses on developing systematic understanding of functions through graphing, developing number sense, representing and solving functions, deepening algebraic manipulation skills, and solving related word problems. Topics include linear functions, quadratics, transformations, complex numbers, polynomials, rational equations, and exponential and logarithmic functions. Students grow in their capacity to puzzle through unfamiliar problems, with an emphasis on real-world applications of the mathematical concepts they are studying.

Prerequisite(s):  B- in Geometry Advanced, A- in Geometry, or (Algebra I with concurrent enrollment in Geometry and Department Approval)

This course covers the core content of Algebra II through a problem-based curriculum that emphasizes learning by doing. The classroom is student-centered, requiring students to explore, experiment, and think flexibly while the teacher acts as a facilitator. Increased theory and open-ended problem solving are prioritized; students are challenged to apply reasoning skills, deepen their mathematical practices, and work collaboratively to solve real-world problems. This course encourages creative thinking and a deeper appreciation for the subject’s complexity, providing a rigorous foundation for AP Precalculus and AP Calculus.

Prerequisite(s): C in Algebra II 

Precalculus is an in depth treatment of the mathematics essential to calculus, with a strong emphasis on trigonometry and functions. The course moves at a measured pace, providing regular opportunities to build fluency, revisit key ideas, and strengthen algebraic foundations. Students study a wide range of function types, including polynomial, rational, exponential, logarithmic, inverse, circular, and trigonometric functions, with attention to domain, range, transformations, and multiple representations. Trigonometric topics include radians, the unit circle, sinusoidal functions and their transformations, inverse trigonometric functions, identities, equations, and triangle trigonometry. Students also analyze polynomial and rational functions, explore conic sections, and study exponential and logarithmic behavior, concluding with an introduction to limits and the definition of the derivative. Throughout the course, emphasis is placed on algebraic fluency, multi step problem solving, graphing technology, and real world applications to prepare students for calculus and related fields.

Prerequisite(s): B- in Algebra II Advanced or A- in Algebra II

Students will explore more deeply many of the algebra concepts they have already seen such as: function notation, domain/range, rational expressions, logs and exponentials, and trigonometry while also learning new topics like matrices, sequences/series, conic sections, polar/parametric equations, and limits. A very strong emphasis will be placed on using the tools of Algebra I & II and Geometry to untangle complex problems so that students are well prepared for the AP Calculus curriculum. Students will be working on both developing a vision for untangling these problems and improving their consistency in applying the rules of algebra. This course will also directly practice the math used in AP Chemistry, AP Biology, and AP Physics.

Please Note: AP courses may require additional meeting times throughout the year.

Prerequisite(s):  B- in AP Precalculus or A- in Precalculus

AP Calculus AB is a college level course that introduces students to differential and integral calculus of single variable functions. The course emphasizes a strong conceptual understanding of limits, continuity, derivatives, and integrals, along with the ability to apply these ideas to analyze change in mathematical and real world contexts. Students study limits and continuity, differentiation and its applications such as related rates, optimization, and curve sketching, and integration with a focus on accumulation, area, and applications. Throughout the course, students work to connect algebraic, graphical, numerical, and verbal representations of functions, and to interpret what calculus results mean in context rather than treating them as purely symbolic answers.

Students work both independently and in small groups to develop fluency with new techniques, encounter unfamiliar problem types, and strengthen their ability to reason through multi-step problems. Emphasis is placed on accurate computation, clear mathematical communication, and the justification of solutions using appropriate calculus concepts. This course is well suited for students who are comfortable working with functions and algebraic expressions, who can persist through challenging problems, and who are interested in building a solid and connected understanding of calculus ideas. By the end of the year, students are prepared for the AP Calculus AB exam and are well positioned to continue on to AP Calculus BC or further study in calculus based mathematics, science, engineering, and other quantitative disciplines. 

Please Note: AP courses may require additional meeting times throughout the year.

Prerequisite(s): B- in AP Calculus AB or A- in AP Precalculus

AP Calculus BC is a one year college level course that includes a rapid review and coverage of all AP Calculus AB topics, followed by an in depth exploration of additional advanced calculus concepts. Students study limits, derivatives, and integrals of single variable functions at an accelerated pace before extending their work to more advanced topics. These include parametric, polar, and vector functions, advanced integration techniques, and the study of sequences and series, including Taylor and Maclaurin series. The course emphasizes both computational skill and conceptual understanding, with a strong focus on connecting multiple representations of functions and using calculus to model and analyze complex mathematical situations.

Students work independently and in small groups to explore new problem types, apply familiar techniques in unfamiliar contexts, and refine their mathematical reasoning. The course places a strong emphasis on accuracy, persistence, and clear communication of mathematical ideas, particularly when working through multi-step and abstract problems. AP Calculus BC is well suited for students who are comfortable moving quickly through core calculus ideas, who enjoy engaging deeply with challenging problems, and who are interested in a more comprehensive and rigorous calculus experience. By the end of the year, students are prepared for the AP Calculus BC exam and for advanced study in mathematics, science, engineering, or related fields.

Please Note: AP courses may require additional meeting times throughout the year.

ELECTIVE COURSES

Prerequisite(s):  Algebra II

Statistics is an extremely powerful and often misunderstood mathematical tool which offers many applications to analyzing the real world. This course emphasizes a real-world data, project-based approach. Students will learn how to collect, research, summarize, display, analyze, and communicate written conclusions about data. Students will have opportunities to both do statistical analyses on data and think critically about statistical interpretations and detect flaws in statistical reasoning. Students will also learn to use spreadsheets as a computational tool. The class will focus primarily on statistics and probability, but will also include a final component of real world numerical applications, including learning to do basic taxes, selecting better credit cards, developing a budget, and learning about the time value of money. These other mathematical applications will be covered in a combination of in class learning and individual projects to learn about a selected area of interest.

Please Note: Students who plan to take both Precalculus and Statistics are strongly encouraged to take Precalculus first, immediately upon completion of Algebra II.

MATH COURSE SEQUENCE